HüdromehaanikaHüdromehaanika on mehaanika haru, mis käsitleb vedelike füüsikalisi omadusi ja käitumist staatilises olekus (hüdrostaatika) ja voolavas olekus (hüdrodünaamika). Erinevus vedelike ja tahkete ainete vahel seisneb selles, et vedelikud ei oma kindlat kuju, vaid võtavad neid ümbritseva anuma kuju. Rõhu ülekandmiseks kasutatakse nii gaase kui vedelikke, millede erinevuseks on see, et surve avaldamisel neile muutub gaasi ruumala märksa enam kui vedeliku ruumala. Hüdrostaatika Hüdrostaatika seadused on rakendatavad vaid ideaalsete vedelike korral st. vedelik ei oma kaalu, puudub hõõrdejõud ja vedelik ei ole kokkusurutav. Nende seaduste abil saab hinnata ideaalsete (energiakadudeta) süsteemide käitumise üle. Reaalsetes hüdrosüsteemides tekib aga erinevaid energiakadusid kõikides, süsteemi komponentides. Teatud komponentide kasutamisel, kus toimub vedeliku voolu takistamine, on tekkivad kaod õigu-poolest eelduseks nende funktsio-neerimisele. Rõhk Kui rõhk mõjub võrdse suurusega pindaladele (A1 = A2 = A3) siis tekkivad jõud (F1 = F2 = F3) on võrdsed 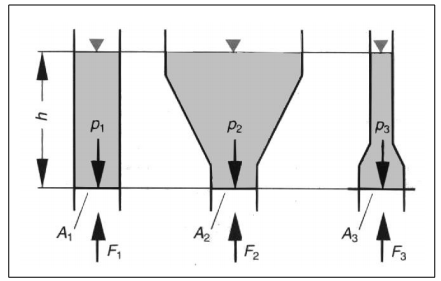 Hüdrostaatika aluseks on Pascali seadus, mille järgi staatilises olekus vedelikule mõjuva jõu poolt tekitatud rõhk mõjub ühtlaselt kogu vedeliku ruumalas. Tekkiva rõhu suurus on võrdne vedelikule mõjuva jõu ja vastava pindala suuruse jagatisega. Kuna tänapäeva hüdrosüsteemides on kasutusel suhteliselt suured rõhud, siis võib neis üldjuhul jätta raskusjõu poolt põhjustatud rõhu mõju arvestamata. Pascali seadus: 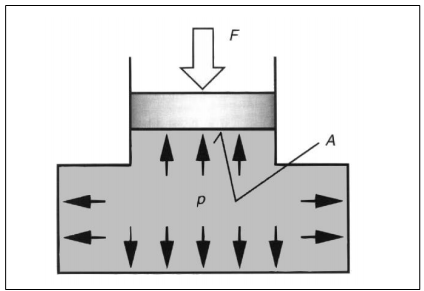 Jõu muundamine Kuna rõhk mõjub ühtlaselt kogu vedeliku ruumalas ei oma anuma kuju rõhu suurusele mingit tähtsust. 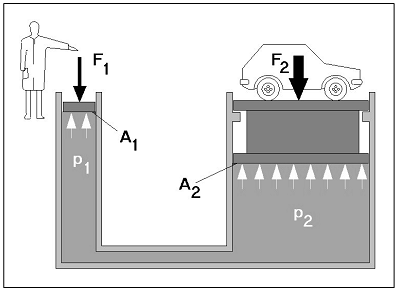 Kui jõud F1 mõjub kolvile pindalaga A1, siis tekitab see anumas rõhu suurusega: p = F1 / A1 See rõhk mõjudes omakorda kolvile pindalaga A2 tekitab jõu F2 suurusega: F2 = p x A2 Seega = F1 / A1 = F2 / A2 või = F2 / F1 = A1 / A2 Jõudude F1 ja F2 suhe on võrdne kolbide pindalade A1 ja A2 suhtega. Suurendades jõudu F1 suureneb rõhk süsteemis väärtuseni mille juures rõhu p toimel hakkab kolb pindalaga A2 liikuma ületades jõu F2. Seega juhul kui jõu F1 ja pindala A1 abil on võimalik tekitada piisav rõhk jõu F2 ületamiseks on võimalik tõsta koormusi. (Hõõrdejõudu siin ei arvestatud.) 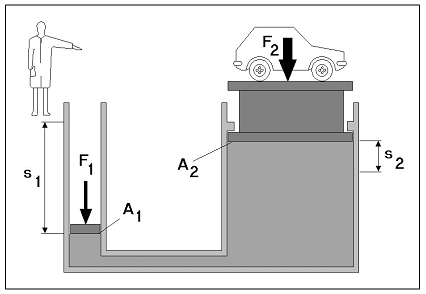 Kolbide liikumisteekonnad s1 ja s2 on omavahel pöördvõrdelises sõltuvuses kolbide pindaladega: s1 / s2 = A2 / A2 Kolvi (1) poolt sooritatud töö W1 on sama suur kui kolvi (2) poolt sooritatud töö W2: W1= F1 x s1 W2= F2 x s2 Rõhu muundamine 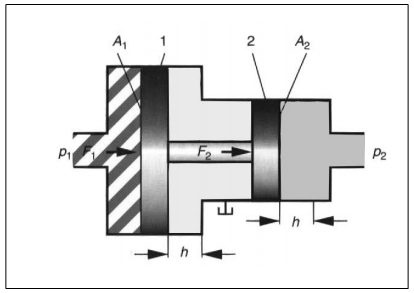 Kaks erineva pindalaga kolbi (1 ja 2) on omavahel seotud ühise kolvivarrega (sele 2.8). Kui kolvile 1 pindalaga A1 mõjub rõhk p1 saadakse tulemusena jõud F1, mis kolvivarre kaudu mõjudes kolvile 2 pindalaga A2, tekitab silindris 2 rõhu p2. Arvestamata takistusjõude saame: F1 = F2 ja p1 x A1 = p2 x A2 siit p1 x A1 = F1 ja p2 x A2 = F2 või p1 / p2 = A2 / A2 Rõhumuundajas toimub rõhu suuruse muutmine pöördvõrdeliselt kolbide pindaladele. Hüdrokineetika Hüdrokineetika käsitleb vedelike voolamisseadusi ja voolamist põhjus-tavaid jõude. Hüdrokineetika abil saab arvutada ka hüdrostaatikas esinevaid kadusid. Kui mitte arvestata vedeliku pinnal ja vedelikus endas esinevaid hõõrdejõude, võib voolamisprotsessi lugeda ideaalseks. Edasi me käsitlemegi ideaalset voolamisprotsessi, kuna seda on võimalik kirjeldada piisavalt täpselt. Voolamisseadus 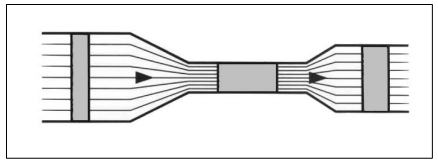 Torus voolava vedeliku kogus mingil ajahetkel on toru igas punktis ühesugune Vedeliku vooluhulk Q saadakse jagades vedeliku ruumala V ajaga t: Q = V/t Vedeliku kogus V saadakse korrutades toru ristlõike A pikkusega s : V = A x s Kui asendada V x A x s siis saame: Q = (A x s) / t Jagades teekonna s ajaga t saame vedeliku voolukiiruse: v = s / t Vooluhulk Q on seega toru ristlõike-pindala A ja voolukiiruse v korrutis 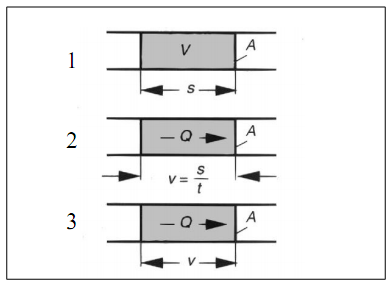 Kuna vooluhulk on torustiku igas punktis ühesugune, siis juhul kui torustiku ristlõige on torustiku erinevates punktides erinev (A1 ja A2) siis voolukiirused nendes punktides on vastavalt (sele 2.11): Q1 = Q2 Q1 = A1 x V1 Q2 = A2 x V2 seega A1 x V1 = A2 x V2 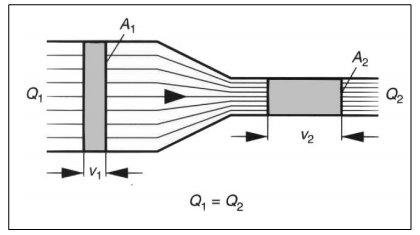 Bernoulli võrrand Rakendades voolavale vedelikule energia jäävuse seadust saame, et voolava vedeliku koguenergia ei muutu niikaua kuni seda väljastpoolt ei lisata või ei eemaldata. Jättes kõrvale need energialiigid, mis ei muundu saame et, koosneb vedeliku koguenergia: - potentsiaalsest energiast, mis sõltub vedeliku samba kõrgusest ja staatilisest rõhust ning - kineetilisest energiast, mis sõltub vedeliku voolu kiirusest ja rõhkude vahest. Siit saadakse Bernoull’i võrrand: g x h + p / q + v2 / 2 = const. Sama võrrand kujul rõhk-energia saadakse: ptot = pst + q x g x h + p / 2 x v2, kus pst - staatiline rõhk q x g x h - vedelikusamba kõrgusest põhjustatud rõhk p / 2 x v2 - dünaamiline rõhk Energia jäävuseseadusest ja Bernoull’i võrrandist järeldub et, vedeliku voolukiiruse kasvades torustiku ristlõikepindala vähenemise tulemusena, kasvab vedeliku kineetiline energia. Kuna vedeliku koguenergia püsib muutumatuna, siis potentsiaalne energia ja/või rõhk vähenevad. Kui vedeliku voolukiirus väheneb torustiku ristlõikepindala suurenemise tulemusena, siis vedeliku kineetiline energia väheneb. Kuna kogu energia jääb samaks siis potentsiaalne energia ja/või rõhk peab suurenema Hõõrdekaod ja rõhulangus torustikus 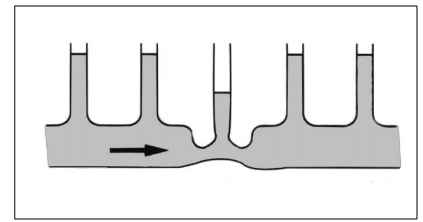 Seni oleme vaadelnud loodusseadusi arvestamata, et igas süsteemis esinevad ka takistusjõud nii torustiku pinna ja vedeliku vahel kui ka vedeliku enda kihtide vahel. Praktikas on võimatu ülekanda hüdroenergiat ilma kadudeta. Tänu hõõrdejõududele tekib vedeliku voolamisel soojus, st hüdroenergia muutub soojuseks. Sellisel moel tekkinud kaod tähendavad praktikas seda, et torustikus tekib rõhulangus. Rõhulangust tähistatakse p. Mida suurem on hõõrdetakistus vedelikus endas, seda suurem on tema viskoossus 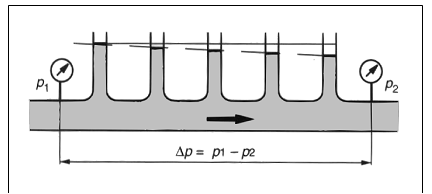 Hõõrdekaod torustikus sõltuvad järgmis-test teguritest nagu: - torustiku pikkus - torustiku ristlõige - torustiku pinnakaredus - liidete arv torustikus - vedeliku voolukiirus - vedeliku viskoossus Vedelike voolamise tüübid Tähtsaks teguriks hüdrosüsteemide energiakadude uurimisel on vedeliku voolamise uurimine. Käsitletakse kahte tüüpi voolamist: - laminaarne voolamine - turbulentne voolamine. Teatava voolukiiruseni liigub vedelik torustikus ühesuunaliselt (laminaarselt). Toru keskel on voolukiirus suurim, pinnal aga null. Kui suurendada vedeliku voolukiirust, siis teatava kriitilise kiiruse juures voolamise tüüp muutub ja voolavas vedelikus tekivad pöörised. Sellise voolamise korral suurenevad järsult voolutakistus ja hüdraulilised kaod. Seetõttu ei ole turbulentne voolamine praktikas soovitud. See kriitiline voolukiirus ei ole konstantne suurus, vaid ta sõltub vedeliku viskoossusest ja toru ristlõike-pindalast. Kriitilist kiirust on võimalik välja arvutada ja seda ei tohiks hüdro-torustikus ületada. 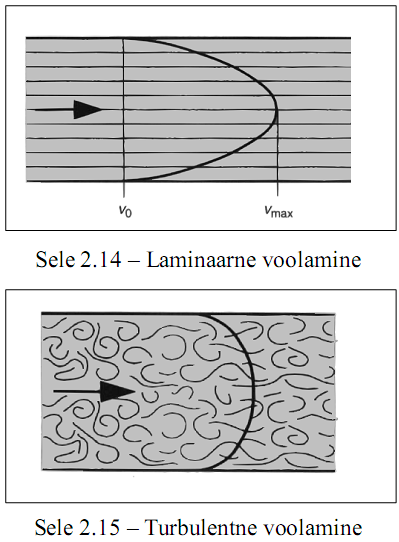 Reynoldsi arv Re Voolamise tüübi üle saab otsustada ligikaudselt Reynoldsi arvu abil: Re = (v x dh) / v kus v - Voolukiirus m/s dh - hüdrauliline läbimõõt [m], ringikujulise ristlõike korral võrdne toru siseläbimõõduga, teistel juhtudel: dh = 4 x A/U A - toru ristlõike pindala U - toru pikkus v -kinemaatiline viskoossus m2/s Rekr - 2300, milline väärtus kehtib ainult ümmargustele, siledaseinaliste ja sirgete torude korral. Rekr juures toimub laminaarse voolamise muutumine turbulentseks ja vastupidi. Voolamine on laminaarne kui Re < Rekr ja turbulentne kui Re > Rekr. |
Seaded |
|
Viimane uuendus: 17.10.2012 20:22:48 |
Kontakt |
| Pärnumaa Kutsehariduskeskus |
powered by cmsimple.dk
- template by cmsimple-styles.com |